 Най-бързият път
Най-бързият път
Това са няколко разсъждения на тема "търси и намери", свързани с игровите ситуации.
Те имат практически характер.
По подразбиране игрите са просто подобие на живо поведение.
Предната статия на тази тема (виж за най-късия път) е геометрична
и разчита на векторен тип карта.
Преди няколко месеца намерих едно решение за точкови карти, което ми се стори интересно,
затова го публикувам тук, в раздел "други безполезни".
То показва убедително, че най-бързият път е доста различен от най-късия.
Като инструмент за изследване написах една примерна програма, чиито резултат се вижда по-долу.
Условието на задачата е:
Дадена е карта съставена от квадратни полета, за които се предполага че са стъпки при движението
на фигурите, както и неделими рисунки от екранния образ.
Някои от полетета са непроходими /недостъпни/.
Едно от полетата на картата е обявено за цел.
Играчът се намира върху друго поле.
Да се намери маршрут (поредица съседни и достъпни полета), по които се движи играчът за да достигне целта.
Забележка:
Има два случая за дефиниция на съседство:
1. Две полета са съседни, когато имат обща страна.
2. Две полета са съседни, когато имат обща точка.
Първият случай е общоприет, затова ще го предполагаме по-долу. Иначе те имат еднотипно решение.
Примерната програма генерира случайно непроходимите/тъмни/ полета, както и двете позиции -
играч и цел. Играчът е в червено, а целта в зелено - фиг.1

фиг.1
Изискване към този тип програми е да работят много бързо /могат да стигнат до стотици изследвания за един кадър/.
Затова е добре да изберем просто изследване. Избраното тук се състои в подбора на това съседно поле, което е достъпно и е най-близо до целта.
По-долу на фиг. 2, с S1, S2, S3 са означени трите пътя, които се изследват по ред от най-къс към най-дълъг. В рамките на точката се приема, че дължината на пътя е геометрично разстояние.
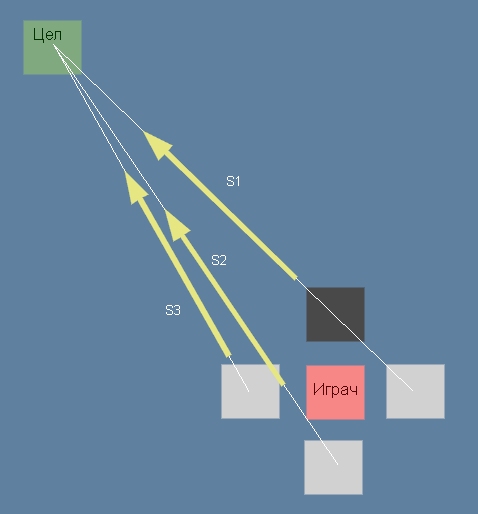
фиг.2
Да забележим, че има съществена вероятност движение от подобни съображения да доведе до задънена улица
и това със сигурност ще провали успеха на цяла поредица ходове.
Обаче действията имат статистически определен изход, което рязко подобрява шанса на
играча. Процесът се илюстрира от следващите три кадъра:


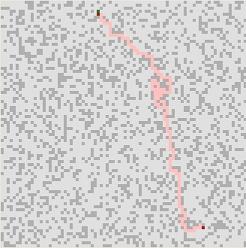
фиг.3,4,5
Като цяло резултатът е приемлив. В почти 95 процента от случаите намерената пътека се различава от най-късата с по-малко от 15 процента.
В около 4 процента от случаите тази грешка е 16-30 процента. Има около един процент вероятност пътеката да е доста далеч от най-късата.
Инструменталната програма е тук - един файл 380к lab.exe.
________________________________________________________________________________________
Радостин Желязков 13.12.2008
Други статии
 Най-бързият път
Най-бързият път




